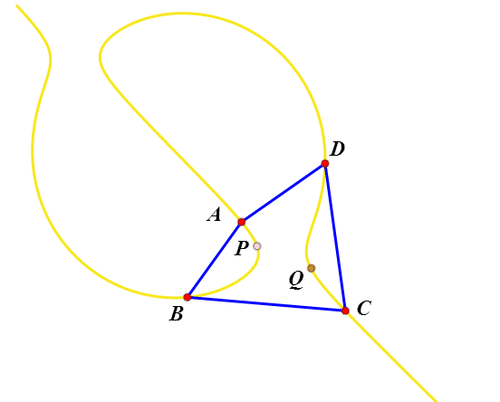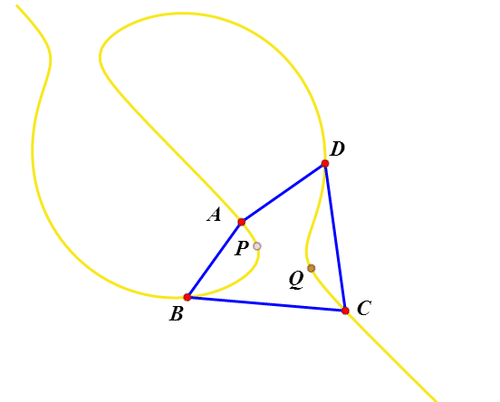
1、理论基础——把四边形ABCD放到复平面上,P关于ABCD存在等角共轭点的等价条件是:(P-A)/(P-B)*(P-C)/(P-D)为实数。
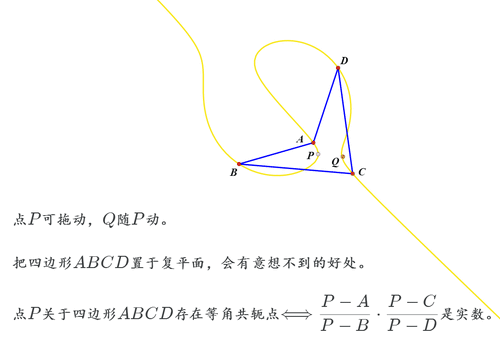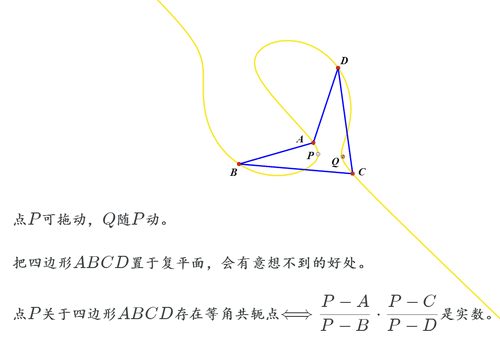
2、打开网络画板,绘制任意四边形ABCD;分别测量四个顶点的坐标。
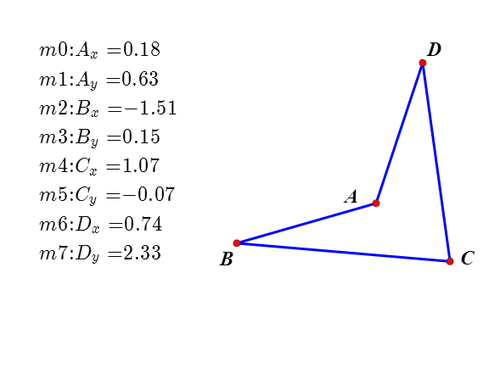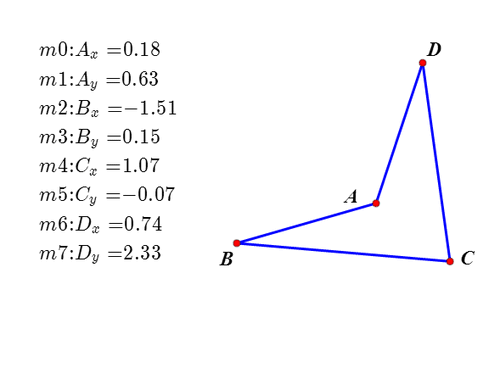
3、打开Mathematica,输入如下代码:a = m0 + I m1;b = m2 + I m3;c = m4 + I m5;d = m6 + I m7;p = x + I y;这是把图形置于复平面时每个点对应的复数,其中p代表P的位置。

4、那么,p存在等角共轭点的等价条件是((p - a)/(p - b))*((p - c)/(p - d))是实数,也就是((p - a)/(p - b))*((p - c)/(p - d))的虚部为0。这样就可以用Mathematica求出p的轨迹的隐函数方程,这是一个三次方程。

5、在网络画板里面画出这个隐函数方程。由于这个隐函数方程的表达式太长了,可能出图的时候会有点卡顿。
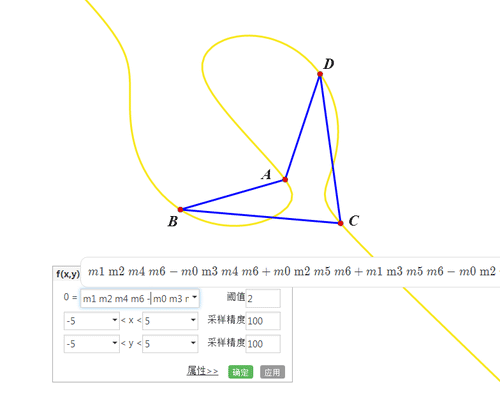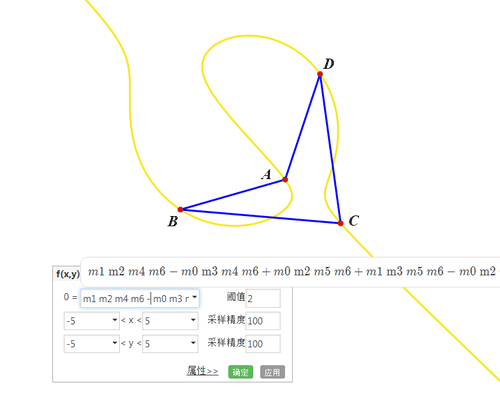
6、这个轨迹经过A、B、C、D四点;这个轨迹上任意点P,都有唯一的Q作为P的等角共轭点,而且Q也在这个轨迹上;不过,当P靠近四边形顶点的时候,Q会出现混乱,似乎出现跳脱现象。
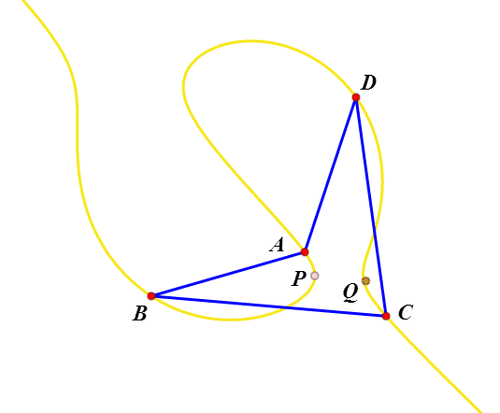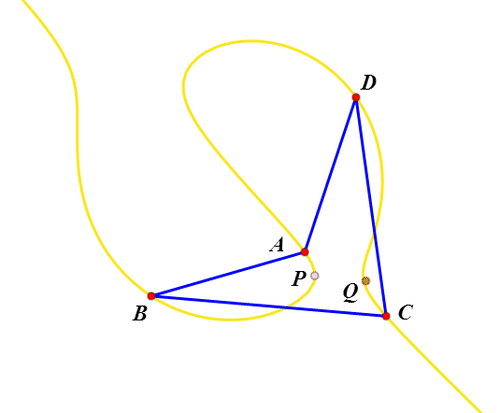
7、改变四边形的形状,轨迹曲线也随之而变;轨迹曲线有时候是一个整体,有时候又会化为两个分支。
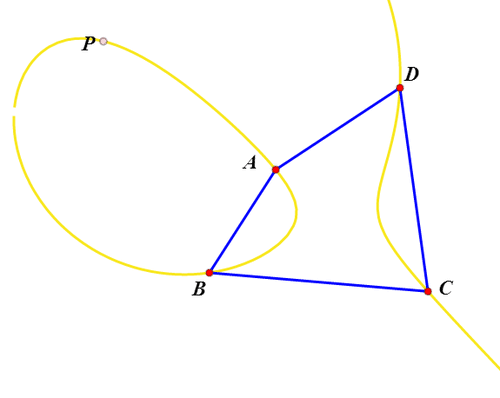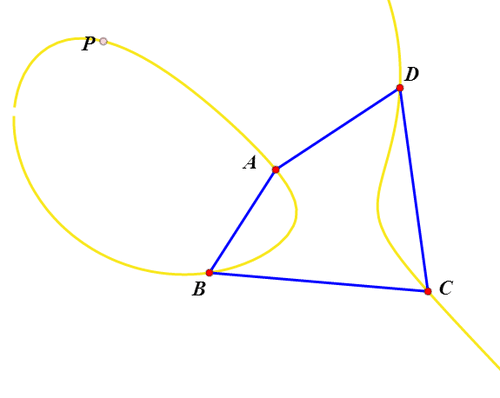
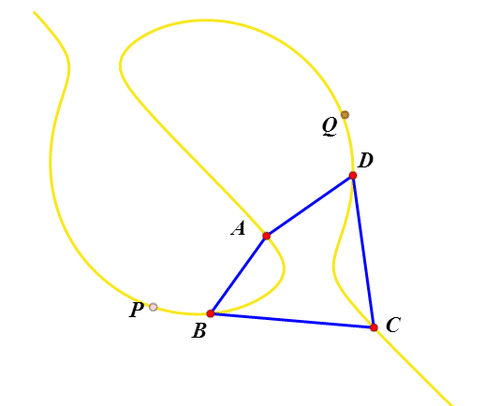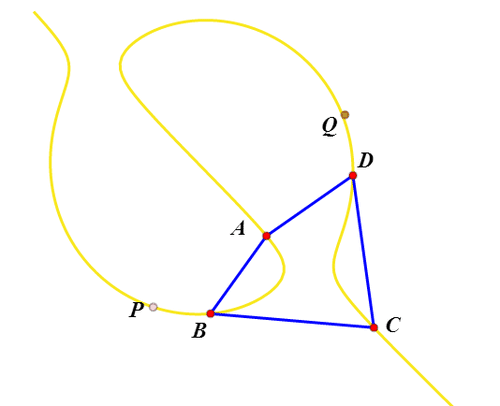
8、还有一点比较有趣,当P在四边形内部,Q也必定一样。